Descriptive Statistics
Table of contents
Frequency Tables
Frequency tables can be used for all kinds of variables, however, it’s preferable to use them for the categorical ones. If you use it for numerical data, the variable’s values have to be divided into ranges.
To get an absolute frequency table using R,
the easiest way is by using the function table(),
and for a relative frequency table prop.table().
table(data$Gender) # Creates an absolute frequency table of Gender
##
## Female Male
## 21 40
table(data$Status)
##
## Bipolar disorder Healthy control
## 30 31
require(magrittr) # Allows using pipe inside R
## Loading required package: magrittr
table(data$Gender) %>% # Pipes the absolute freq. table into
prop.table() # a relative freq. table
##
## Female Male
## 0.3442623 0.6557377
Try: What happens if we ask for a prop.table() on an object that is not a table?
# prop.table(data$Gender)
The table() function also allows us to create cross-tables. For that, the input is two variables.
table(data$Gender, data$Status)
##
## Bipolar disorder Healthy control
## Female 14 7
## Male 16 24
table(data$Gender, data$Status) %>%
prop.table(.) %>%
round(.,2)
##
## Bipolar disorder Healthy control
## Female 0.23 0.11
## Male 0.26 0.39
When the interest lies in visualising this results, the barplot() can be used to represent visually a frequency table.
table(data$Gender, data$Status) %>%
barplot(., beside = TRUE,
legend.text = TRUE,
col = c('salmon','turquoise'),
args.legend = list(x = 'topleft',
bty = 'n'),
ylim = c(0,25),
las = 1)

Central tendency measures
Central tendency measures attempts to summarise/describe the dataset by its central position. The mean, median and mode are examples of central measurements.
The five-number summary is a set of descriptive statistics that provide information about a dataset. It consists of five quartiles:
- $Q_0$ the lowest value of the sample, aka Minimum
- $Q_1$ $25\%$ of the sample, aka lower quantile
- $Q_2$ $50\%$ of the sample, aka median
- $Q_3$ $75\%$ of the sample, aka upper quantile
- $Q_4$ the biggest value of the sample, aka Maximum
The functions summary() and fivenum() returns the five-number summary. They are a bit different how they calculate the $1^{st}$ and $3^{rd}$ quantiles.
summary() calculates the average of the two numbers, if even, fivenum() returns the minimum.
### The function summary will give you an overview of the full data set if you want to!
summary(data)
## X Age_death Age_onset Alcohol_abuse
## GSM123182: 1 Min. :19.00 Min. :14.00 Min. :0.000
## GSM123183: 1 1st Qu.:38.00 1st Qu.:18.25 1st Qu.:0.000
## GSM123184: 1 Median :45.00 Median :22.00 Median :1.000
## GSM123185: 1 Mean :44.18 Mean :24.03 Mean :1.817
## GSM123186: 1 3rd Qu.:49.00 3rd Qu.:27.75 3rd Qu.:3.250
## GSM123187: 1 Max. :64.00 Max. :45.00 Max. :5.000
## (Other) :55 NA's :31 NA's :1
## Brain_ph Status Drug_abuse Duration_illness
## Min. :5.920 Bipolar disorder:30 Min. :0.0000 Min. : 2.00
## 1st Qu.:6.400 Healthy control :31 1st Qu.:0.0000 1st Qu.:14.00
## Median :6.600 Median :0.0000 Median :18.50
## Mean :6.553 Mean :0.1935 Mean :20.50
## 3rd Qu.:6.740 3rd Qu.:0.0000 3rd Qu.:27.75
## Max. :7.030 Max. :3.0000 Max. :45.00
## NA's :30 NA's :31
## Therapy_Electroconvulsive Therapy_Fluphenazine Gender
## No :28 Min. : 0 Female:21
## Yes : 2 1st Qu.: 0 Male :40
## NA's:31 Median : 3000
## Mean : 11283
## 3rd Qu.: 12000
## Max. :130000
## NA's :32
## Therapy_Lithium Post_morten_interval Side_brain Suicide
## No :22 Min. : 9.00 Left :32 No :49
## Yes : 8 1st Qu.:23.00 Right:29 Yes:12
## NA's:31 Median :31.00
## Mean :33.05
## 3rd Qu.:39.00
## Max. :84.00
##
## Therapy_Valproate APOLD1 CLDN10 DUSP4
## No :20 Min. :1.765 Min. :1.822 Min. :1.445
## Yes :10 1st Qu.:1.917 1st Qu.:1.984 1st Qu.:1.522
## NA's:31 Median :1.957 Median :2.042 Median :1.562
## Mean :1.997 Mean :2.042 Mean :1.573
## 3rd Qu.:2.113 3rd Qu.:2.113 3rd Qu.:1.632
## Max. :2.286 Max. :2.181 Max. :1.718
##
## EFEMP1 ETNPPL GJA1 PLSCR4
## Min. :1.585 Min. :1.903 Min. :1.840 Min. :1.683
## 1st Qu.:1.766 1st Qu.:2.115 1st Qu.:2.154 1st Qu.:1.861
## Median :1.847 Median :2.194 Median :2.235 Median :1.905
## Mean :1.835 Mean :2.183 Mean :2.219 Mean :1.903
## 3rd Qu.:1.916 3rd Qu.:2.278 3rd Qu.:2.309 3rd Qu.:1.971
## Max. :2.049 Max. :2.367 Max. :2.409 Max. :2.079
##
## SDC4 SLC14A1 SOX9 SST
## Min. :1.740 Min. :1.156 Min. :1.819 Min. :1.782
## 1st Qu.:1.984 1st Qu.:1.291 1st Qu.:1.981 1st Qu.:2.083
## Median :2.028 Median :1.320 Median :2.063 Median :2.172
## Mean :2.021 Mean :1.340 Mean :2.040 Mean :2.137
## 3rd Qu.:2.087 3rd Qu.:1.400 3rd Qu.:2.109 3rd Qu.:2.206
## Max. :2.178 Max. :1.669 Max. :2.237 Max. :2.277
##
## TAC1 CX3CR1 DDX3Y ETNPPL.1
## Min. :1.549 Min. :1.749 Min. :1.397 Min. :1.903
## 1st Qu.:1.837 1st Qu.:1.865 1st Qu.:1.484 1st Qu.:2.115
## Median :1.911 Median :1.979 Median :1.764 Median :2.194
## Mean :1.885 Mean :1.974 Mean :1.674 Mean :2.183
## 3rd Qu.:1.974 3rd Qu.:2.072 3rd Qu.:1.807 3rd Qu.:2.278
## Max. :2.071 Max. :2.263 Max. :1.891 Max. :2.367
##
## G3BP2 GABRG2 KDM5D MAFB
## Min. :1.790 Min. :1.722 Min. :1.494 Min. :1.660
## 1st Qu.:1.937 1st Qu.:1.974 1st Qu.:1.677 1st Qu.:1.869
## Median :1.994 Median :2.088 Median :1.959 Median :1.919
## Mean :1.988 Mean :2.061 Mean :1.863 Mean :1.900
## 3rd Qu.:2.044 3rd Qu.:2.166 3rd Qu.:2.000 3rd Qu.:1.951
## Max. :2.117 Max. :2.245 Max. :2.054 Max. :2.047
##
## NBEA OXR1 PAK1 PCDH8
## Min. :1.868 Min. :1.622 Min. :1.333 Min. :1.727
## 1st Qu.:2.089 1st Qu.:1.896 1st Qu.:1.584 1st Qu.:1.941
## Median :2.110 Median :1.983 Median :1.709 Median :1.997
## Mean :2.094 Mean :1.951 Mean :1.679 Mean :1.986
## 3rd Qu.:2.143 3rd Qu.:2.030 3rd Qu.:1.784 3rd Qu.:2.053
## Max. :2.202 Max. :2.151 Max. :1.901 Max. :2.113
##
## PPID PVALB RPS4Y1 SST.1
## Min. :1.808 Min. :1.779 Min. :1.640 Min. :1.782
## 1st Qu.:1.986 1st Qu.:1.987 1st Qu.:1.768 1st Qu.:2.083
## Median :2.017 Median :2.052 Median :2.227 Median :2.172
## Mean :2.004 Mean :2.030 Mean :2.065 Mean :2.137
## 3rd Qu.:2.051 3rd Qu.:2.087 3rd Qu.:2.248 3rd Qu.:2.206
## Max. :2.109 Max. :2.154 Max. :2.280 Max. :2.277
##
## TAC1.1 TBL1XR1 USP9Y XIST
## Min. :1.549 Min. :1.504 Min. :1.160 Min. :1.424
## 1st Qu.:1.837 1st Qu.:1.742 1st Qu.:1.293 1st Qu.:1.462
## Median :1.911 Median :1.805 Median :1.483 Median :1.497
## Mean :1.885 Mean :1.789 Mean :1.454 Mean :1.701
## 3rd Qu.:1.974 3rd Qu.:1.856 3rd Qu.:1.589 3rd Qu.:2.106
## Max. :2.071 Max. :1.990 Max. :1.796 Max. :2.264
##
### or just the variable you want.
summary(data$Age_death)
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 19.00 38.00 45.00 44.18 49.00 64.00
### (minimum, lower-hinge, median, upper-hinge, maximum)
fivenum(data$Age_death)
## [1] 19 38 45 49 64
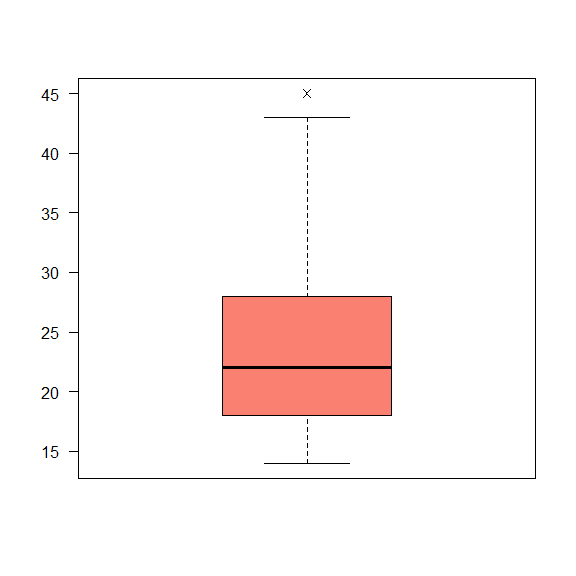
The graphical representation of the summary is the boxplot().
boxplot(data$Age_onset,
las = 2,
pch = 4,
col = 'salmon')
If we are interested in the summary by condition, we can use the function by().
by(data, data$Status,
FUN = summary)
## data$Status: Bipolar disorder
## X Age_death Age_onset Alcohol_abuse
## GSM123182: 1 Min. :19.00 Min. :14.00 Min. :0.000
## GSM123183: 1 1st Qu.:41.00 1st Qu.:18.25 1st Qu.:1.000
## GSM123184: 1 Median :44.00 Median :22.00 Median :3.000
## GSM123185: 1 Mean :44.53 Mean :24.03 Mean :2.862
## GSM123186: 1 3rd Qu.:50.75 3rd Qu.:27.75 3rd Qu.:5.000
## GSM123187: 1 Max. :64.00 Max. :45.00 Max. :5.000
## (Other) :24 NA's :1
## Brain_ph Status Drug_abuse Duration_illness
## Min. :5.920 Bipolar disorder:30 Min. : NA Min. : 2.00
## 1st Qu.:6.355 Healthy control : 0 1st Qu.: NA 1st Qu.:14.00
## Median :6.505 Median : NA Median :18.50
## Mean :6.475 Mean :NaN Mean :20.50
## 3rd Qu.:6.665 3rd Qu.: NA 3rd Qu.:27.75
## Max. :6.970 Max. : NA Max. :45.00
## NA's :30
## Therapy_Electroconvulsive Therapy_Fluphenazine Gender
## No :28 Min. : 0 Female:14
## Yes: 2 1st Qu.: 0 Male :16
## Median : 3000
## Mean : 11283
## 3rd Qu.: 12000
## Max. :130000
## NA's :1
## Therapy_Lithium Post_morten_interval Side_brain Suicide
## No :22 Min. :12.00 Left :18 No :18
## Yes: 8 1st Qu.:23.25 Right:12 Yes:12
## Median :35.00
## Mean :37.17
## 3rd Qu.:47.00
## Max. :84.00
##
## Therapy_Valproate APOLD1 CLDN10 DUSP4
## No :20 Min. :1.807 Min. :1.889 Min. :1.445
## Yes:10 1st Qu.:1.941 1st Qu.:2.006 1st Qu.:1.506
## Median :1.983 Median :2.051 Median :1.540
## Mean :2.024 Mean :2.062 Mean :1.548
## 3rd Qu.:2.117 3rd Qu.:2.136 3rd Qu.:1.572
## Max. :2.286 Max. :2.181 Max. :1.718
##
## EFEMP1 ETNPPL GJA1 PLSCR4
## Min. :1.616 Min. :2.000 Min. :2.014 Min. :1.701
## 1st Qu.:1.796 1st Qu.:2.163 1st Qu.:2.200 1st Qu.:1.890
## Median :1.867 Median :2.204 Median :2.260 Median :1.916
## Mean :1.853 Mean :2.215 Mean :2.244 Mean :1.921
## 3rd Qu.:1.922 3rd Qu.:2.287 3rd Qu.:2.309 3rd Qu.:1.989
## Max. :2.003 Max. :2.367 Max. :2.374 Max. :2.078
##
## SDC4 SLC14A1 SOX9 SST
## Min. :1.855 Min. :1.168 Min. :1.819 Min. :1.782
## 1st Qu.:2.007 1st Qu.:1.309 1st Qu.:2.039 1st Qu.:2.032
## Median :2.058 Median :1.346 Median :2.087 Median :2.093
## Mean :2.051 Mean :1.363 Mean :2.067 Mean :2.084
## 3rd Qu.:2.106 3rd Qu.:1.405 3rd Qu.:2.121 3rd Qu.:2.170
## Max. :2.158 Max. :1.583 Max. :2.237 Max. :2.277
##
## TAC1 CX3CR1 DDX3Y ETNPPL.1
## Min. :1.549 Min. :1.762 Min. :1.397 Min. :2.000
## 1st Qu.:1.771 1st Qu.:1.826 1st Qu.:1.445 1st Qu.:2.163
## Median :1.849 Median :1.961 Median :1.723 Median :2.204
## Mean :1.825 Mean :1.940 Mean :1.627 Mean :2.215
## 3rd Qu.:1.928 3rd Qu.:2.021 3rd Qu.:1.783 3rd Qu.:2.287
## Max. :2.029 Max. :2.149 Max. :1.839 Max. :2.367
##
## G3BP2 GABRG2 KDM5D MAFB
## Min. :1.790 Min. :1.722 Min. :1.494 Min. :1.660
## 1st Qu.:1.903 1st Qu.:1.946 1st Qu.:1.626 1st Qu.:1.810
## Median :1.979 Median :2.050 Median :1.945 Median :1.900
## Mean :1.958 Mean :2.022 Mean :1.814 Mean :1.869
## 3rd Qu.:2.015 3rd Qu.:2.117 3rd Qu.:1.994 3rd Qu.:1.945
## Max. :2.107 Max. :2.240 Max. :2.034 Max. :2.031
##
## NBEA OXR1 PAK1 PCDH8
## Min. :1.868 Min. :1.622 Min. :1.333 Min. :1.727
## 1st Qu.:2.013 1st Qu.:1.845 1st Qu.:1.512 1st Qu.:1.906
## Median :2.101 Median :1.934 Median :1.659 Median :1.965
## Mean :2.061 Mean :1.916 Mean :1.644 Mean :1.953
## 3rd Qu.:2.122 3rd Qu.:1.999 3rd Qu.:1.772 3rd Qu.:2.005
## Max. :2.176 Max. :2.101 Max. :1.882 Max. :2.076
##
## PPID PVALB RPS4Y1 SST.1
## Min. :1.808 Min. :1.779 Min. :1.685 Min. :1.782
## 1st Qu.:1.916 1st Qu.:1.941 1st Qu.:1.755 1st Qu.:2.032
## Median :1.996 Median :2.014 Median :2.201 Median :2.093
## Mean :1.973 Mean :2.000 Mean :2.013 Mean :2.084
## 3rd Qu.:2.017 3rd Qu.:2.073 3rd Qu.:2.235 3rd Qu.:2.170
## Max. :2.097 Max. :2.112 Max. :2.280 Max. :2.277
##
## TAC1.1 TBL1XR1 USP9Y XIST
## Min. :1.549 Min. :1.504 Min. :1.160 Min. :1.434
## 1st Qu.:1.771 1st Qu.:1.682 1st Qu.:1.283 1st Qu.:1.479
## Median :1.849 Median :1.775 Median :1.401 Median :1.534
## Mean :1.825 Mean :1.753 Mean :1.404 Mean :1.791
## 3rd Qu.:1.928 3rd Qu.:1.834 3rd Qu.:1.526 3rd Qu.:2.127
## Max. :2.029 Max. :1.914 Max. :1.680 Max. :2.264
##
## --------------------------------------------------------
## data$Status: Healthy control
## X Age_death Age_onset Alcohol_abuse
## GSM123212: 1 Min. :31.00 Min. : NA Min. :0.0000
## GSM123213: 1 1st Qu.:38.00 1st Qu.: NA 1st Qu.:0.0000
## GSM123214: 1 Median :45.00 Median : NA Median :0.0000
## GSM123215: 1 Mean :43.84 Mean :NaN Mean :0.8387
## GSM123216: 1 3rd Qu.:48.50 3rd Qu.: NA 3rd Qu.:1.0000
## GSM123217: 1 Max. :59.00 Max. : NA Max. :4.0000
## (Other) :25 NA's :31
## Brain_ph Status Drug_abuse Duration_illness
## Min. :6.000 Bipolar disorder: 0 Min. :0.0000 Min. : NA
## 1st Qu.:6.500 Healthy control :31 1st Qu.:0.0000 1st Qu.: NA
## Median :6.700 Median :0.0000 Median : NA
## Mean :6.628 Mean :0.1935 Mean :NaN
## 3rd Qu.:6.810 3rd Qu.:0.0000 3rd Qu.: NA
## Max. :7.030 Max. :3.0000 Max. : NA
## NA's :31
## Therapy_Electroconvulsive Therapy_Fluphenazine Gender
## No : 0 Min. : NA Female: 7
## Yes : 0 1st Qu.: NA Male :24
## NA's:31 Median : NA
## Mean :NaN
## 3rd Qu.: NA
## Max. : NA
## NA's :31
## Therapy_Lithium Post_morten_interval Side_brain Suicide
## No : 0 Min. : 9.00 Left :14 No :31
## Yes : 0 1st Qu.:21.50 Right:17 Yes: 0
## NA's:31 Median :28.00
## Mean :29.06
## 3rd Qu.:36.50
## Max. :58.00
##
## Therapy_Valproate APOLD1 CLDN10 DUSP4
## No : 0 Min. :1.765 Min. :1.822 Min. :1.469
## Yes : 0 1st Qu.:1.889 1st Qu.:1.974 1st Qu.:1.538
## NA's:31 Median :1.942 Median :2.026 Median :1.618
## Mean :1.971 Mean :2.022 Mean :1.597
## 3rd Qu.:2.065 3rd Qu.:2.097 3rd Qu.:1.656
## Max. :2.284 Max. :2.146 Max. :1.707
##
## EFEMP1 ETNPPL GJA1 PLSCR4
## Min. :1.585 Min. :1.903 Min. :1.840 Min. :1.683
## 1st Qu.:1.760 1st Qu.:2.067 1st Qu.:2.127 1st Qu.:1.848
## Median :1.804 Median :2.166 Median :2.199 Median :1.883
## Mean :1.817 Mean :2.152 Mean :2.196 Mean :1.885
## 3rd Qu.:1.902 3rd Qu.:2.242 3rd Qu.:2.302 3rd Qu.:1.957
## Max. :2.049 Max. :2.329 Max. :2.409 Max. :2.079
##
## SDC4 SLC14A1 SOX9 SST
## Min. :1.740 Min. :1.156 Min. :1.842 Min. :1.996
## 1st Qu.:1.963 1st Qu.:1.269 1st Qu.:1.966 1st Qu.:2.172
## Median :2.003 Median :1.300 Median :2.018 Median :2.197
## Mean :1.992 Mean :1.318 Mean :2.013 Mean :2.189
## 3rd Qu.:2.045 3rd Qu.:1.339 3rd Qu.:2.087 3rd Qu.:2.225
## Max. :2.178 Max. :1.669 Max. :2.194 Max. :2.275
##
## TAC1 CX3CR1 DDX3Y ETNPPL.1
## Min. :1.760 Min. :1.749 Min. :1.440 Min. :1.903
## 1st Qu.:1.897 1st Qu.:1.923 1st Qu.:1.722 1st Qu.:2.067
## Median :1.945 Median :1.987 Median :1.770 Median :2.166
## Mean :1.944 Mean :2.006 Mean :1.720 Mean :2.152
## 3rd Qu.:1.996 3rd Qu.:2.098 3rd Qu.:1.810 3rd Qu.:2.242
## Max. :2.071 Max. :2.263 Max. :1.891 Max. :2.329
##
## G3BP2 GABRG2 KDM5D MAFB
## Min. :1.898 Min. :1.840 Min. :1.543 Min. :1.760
## 1st Qu.:1.959 1st Qu.:2.024 1st Qu.:1.921 1st Qu.:1.901
## Median :2.035 Median :2.139 Median :1.977 Median :1.938
## Mean :2.018 Mean :2.099 Mean :1.909 Mean :1.931
## 3rd Qu.:2.069 3rd Qu.:2.180 3rd Qu.:2.000 3rd Qu.:1.961
## Max. :2.117 Max. :2.245 Max. :2.054 Max. :2.047
##
## NBEA OXR1 PAK1 PCDH8
## Min. :2.029 Min. :1.641 Min. :1.431 Min. :1.866
## 1st Qu.:2.097 1st Qu.:1.963 1st Qu.:1.646 1st Qu.:1.987
## Median :2.134 Median :2.005 Median :1.723 Median :2.021
## Mean :2.125 Mean :1.985 Mean :1.713 Mean :2.019
## 3rd Qu.:2.148 3rd Qu.:2.036 3rd Qu.:1.799 3rd Qu.:2.063
## Max. :2.202 Max. :2.151 Max. :1.901 Max. :2.113
##
## PPID PVALB RPS4Y1 SST.1
## Min. :1.916 Min. :1.930 Min. :1.640 Min. :1.996
## 1st Qu.:2.014 1st Qu.:2.003 1st Qu.:2.209 1st Qu.:2.172
## Median :2.045 Median :2.081 Median :2.233 Median :2.197
## Mean :2.034 Mean :2.060 Mean :2.115 Mean :2.189
## 3rd Qu.:2.056 3rd Qu.:2.103 3rd Qu.:2.249 3rd Qu.:2.225
## Max. :2.109 Max. :2.154 Max. :2.270 Max. :2.275
##
## TAC1.1 TBL1XR1 USP9Y XIST
## Min. :1.760 Min. :1.632 Min. :1.160 Min. :1.424
## 1st Qu.:1.897 1st Qu.:1.761 1st Qu.:1.393 1st Qu.:1.450
## Median :1.945 Median :1.825 Median :1.540 Median :1.484
## Mean :1.944 Mean :1.823 Mean :1.502 Mean :1.615
## 3rd Qu.:1.996 3rd Qu.:1.879 3rd Qu.:1.607 3rd Qu.:1.537
## Max. :2.071 Max. :1.990 Max. :1.796 Max. :2.162
##
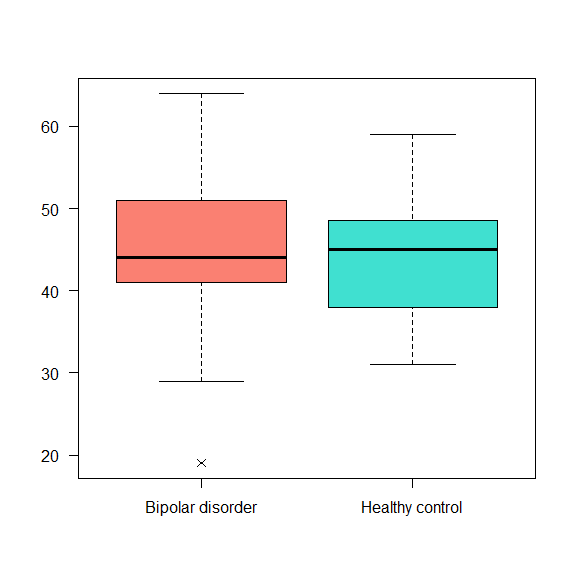
The boxplot() can also be done for two different categories:
boxplot(data$Age_death ~ data$Status,
las = 1, pch = 4,
col = c('salmon', 'turquoise'))
Mean
It is calculated by taking the sum of the values and dividing by the total number of values of the data.
The function mean() can be used to calculate the average.
mean(data$Age_death)
## [1] 44.18033
Interpretation: The average age of death in this study was 44.1803279.
The functions colMeans() and rowMeans() can be also used for computing the mean of columns and rows.
colMeans(data[,c(17:28)], na.rm = T)
## APOLD1 CLDN10 DUSP4 EFEMP1 ETNPPL GJA1 PLSCR4 SDC4
## 1.997240 2.041634 1.572833 1.834842 2.183101 2.219369 1.902763 2.020990
## SLC14A1 SOX9 SST TAC1
## 1.339995 2.039741 2.137336 1.885281
rowMeans(data[,17:28], na.rm = T)
## 1 2 3 4 5 6 7 8
## 2.012922 1.832557 1.840020 1.924146 1.962231 1.981616 1.945479 1.928857
## 9 10 11 12 13 14 15 16
## 1.941477 2.000882 1.874723 1.904858 1.995695 1.974847 1.949153 1.918931
## 17 18 19 20 21 22 23 24
## 1.934290 1.987450 1.958006 1.968084 1.991263 1.920940 1.984736 1.907677
## 25 26 27 28 29 30 31 32
## 1.984528 1.895546 1.952010 1.934318 1.876073 1.858500 1.876398 1.942668
## 33 34 35 36 37 38 39 40
## 1.885970 1.878481 1.817041 1.931009 1.960738 1.963836 1.923612 1.764979
## 41 42 43 44 45 46 47 48
## 1.916670 1.990174 1.864843 1.881532 1.986587 2.011588 1.996816 1.922206
## 49 50 51 52 53 54 55 56
## 1.888220 1.991758 1.944774 1.978649 1.859148 1.978678 1.982875 1.994539
## 57 58 59 60 61
## 1.851342 2.051429 1.809602 1.921640 1.897267
Median
The median is the middle value when a variable is sorted, the functionmedian() computes it in R. When dealing with variables that are not symmetrically distributed, it is important to describe the variable by its median.
median(data$Age_death)
## [1] 45
Interpretation: The mid-age of death in this study was 45. This means that this is the value that divides the data in half.
Note that in the case of non-symmetry, the median is not the same as the mean!
plot((density(data$APOLD1))$x,(density(data$APOLD1))$y,
type = "l",
xlab = "Expression of gene APOLD1",
ylab = "Density",
las = 2,
axes = F,
col = "violet",
lwd = 3,
col.lab = "steelblue")
axis(1,
at = seq(from = (round(min(data$APOLD1))-2), by = 2, to = (2+round(max(data$APOLD1)))),
col = "gray75",
col.axis = "gray75")
axis(2,
las = 2,
col = "gray75",
col.ticks = "gray75",
col.axis = "gray75")
abline(v = median(data$APOLD1),
col = "salmon",
lwd = 2)
abline(v = mean(data$APOLD1),
col = "steelblue",
lwd = 2)
legend("topright",
c(paste("Median", round(median(data$APOLD1),2)), paste("Mean", round(mean(data$APOLD1),2))),
col = c("salmon", "steelblue"),
lwd = 2,
bty = "n")

Mode
The mode is the value that appears the most on a variable. Sometimes, a variable might have more than one mode, but we won’t deal with it here.
Unfortunately, there is no function on R to compute the mode. However, we can construct our own function. By the definition, it is the value that appears the most, so, let’s create a table.
Mode = function(VAR){
actual_mode <- table(VAR)
NAME = names(actual_mode)[actual_mode == max(actual_mode)]
VAL = actual_mode[actual_mode == max(actual_mode)]
return( data.frame(Value = NAME, Frequency = VAL))
}
Mode(data$Age_onset)
Interpretation: The most common age where people were diagnosed with bipolar disorder was 25 years.
Dispersion measures
The dispersion refers to how the values are spread from the central data. It is as important as the central tendency values. Some of them are Range, IQR, Variance and standard deviation.
Range
The range is the difference between the largest and the smallest value of a variable. It means that is the range between the minimum and the maximum of a variable.
The function range() returns the minimum and maximum values, to have the range we have to use the function diff().
range(data$Age_death) %>%
diff(.)
## [1] 45
Interpretation: The difference (or the range) among the ages in our study was 45 years.
Interquartile range (IQR)
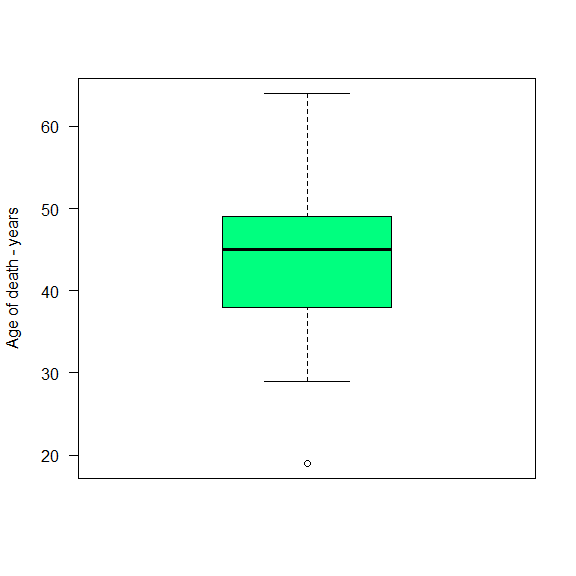
Is the difference between the third and the first quartiles. It’s used to read and draw the boxplots. When dealing with non-symmetrical variables, it is also used to describe its dispersion, instead of using the standard deviation.
On R we can use the function IQR()
IQR(data$Age_death)
## [1] 11
Interpretation: The Interval interquantile is 11. It means that the distance between the $1^{st}$ and $3^{rd}$ quantiles is 11 years. This value can be used to make the interpretation of the boxplot.
boxplot(data$Age_death ,
col = c ("springgreen"),
ylab = "Age of death - years",
las = 2)
quantile(data$Age_death)
## 0% 25% 50% 75% 100%
## 19 38 45 49 64
Variance
Variance is the expectation of the squared deviation of a random variable from its mean. In other words, the variance is how far the values are from the mean. We can calculate it using the function var().
var(data$Age_death)
## [1] 82.38361
Interpretation: The age of the individuals in our study deviates from the mean in 82.38 years$^2$ (quadratic scale).
However, it is quite hard to make interpretations in years$^2$.
Standard deviation (SD)
Is how the values are spread around the mean. It is given by the square root of the variance. A low standard deviation indicates that the data points tend to be close to the mean, while a high standard deviation indicates that the data points are spread out over a wider range of values. To compute the SD using R we can use the function sd().
sd(data$Age_death)
## [1] 9.076542
sqrt(var(data$Age_death))
## [1] 9.076542
Interpretation: The age of the individuals in our study deviates from the mean in 9.08 years (data scale).
Coefficient of variation
The coefficient of variation is the sd divided by the mean. In chemistry is widely used to express the precision and repeatability of an experiment. Normally it is expressed as a percentage. The CV aims to describe the dispersion of the variable in a way that does not depend on the variable’s measurement unit. The higher the CV, the greater the dispersion in the variable.
It’s also used to compare the variation of variables that are not on the same scale.
The R doesn’t have a function to compute it, but we can easily create our own.
sd(data$Age_death)/mean(data$Age_death)*100
## [1] 20.54431
CV <- function(VAR){
(sd(VAR, na.rm = T)/mean(VAR, na.rm = T))*100
}
CV(data$Age_death)
## [1] 20.54431
Exercises
-
Make absolute and relative frequency tables for the variables: Gender and Status.
-
Check how many people that suffered from Bipolar Disorder committed suicide. Visualise it using a barplot.
-
Compute and make the correct interpretations for the mean, median, IQR, standard deviation, variance and CV for all the quantitative variables. Tipp: You can create a function for that!
-
Compute and make the correct interpretations for the mean, median, IQR, standard deviation, variance and CV for all the numeric variables only for Males. Tipp: Use the function created before on a subset of the dataset.
-
Compute and make the correct interpretations for the mean, median, IQR, standard deviation, variance and CV for all the quantitative variables for both conditions separately. Tipp: Use the function created before; use the function
by().