Chapter 4 Method for drug-repurpusing
In this Chapter, we will learn how to calculate the proximity of a drug to a disease - and infer drug repurpusing (Session 4.1)- based on network methodologies.
There are different methods that are used for drug-repurpusing based on networks, such as the diffusion state distance (DSD) (Cao et al. 2013), that uses a graph diffusion property to derive a similarity metric for pairs of nodes, it takes into account how their similarly affect the rest of the network; and AI-based methods, where a heterogeneous graph \(G = (V,R)\) with N nodes \(v_i \in V\) representing distinct types of biomedical entities and labeled edges representing semantically distinct types of edges between the entities (i.e., protein-protein interactions, drug-target associations, disease-protein associations, and drug-disease indications) and are tasked to predict drugs for a particular disease (Zitnik, Agrawal, and Leskovec 2018). Due to the limited time, we will focus only on the proximity-based method.
For this, we will be using the R package NetSci and to make the appropriate visualizations we will use igraph.
4.1 Proximity
Given G, the set of Disease-Genes, T, the set of drug targets, and d(g,t), the shortest path length between nodes \(g \in G\) and \(t \in T\) in the network, the proximity can be defined as (Guney et al. 2016):
\[ d(g,t) = \frac{1}{|\left|T\right||}\sum_{t\in T}\underset{v\in V}\min{d(g,t)}. \]
A visual representation of the method can be seen in Figure 4.1.
The proximity for drug 2 to the disease is calculated by the average of the shortest path from its targets to the disease genes. The shortest path from N to D is 1, from F to D is 3, the average is 2.
For Drug 1, we have: \[d(Drug_1, disease) = \frac{2 + 2 + 1}{3} = 1.66.\]
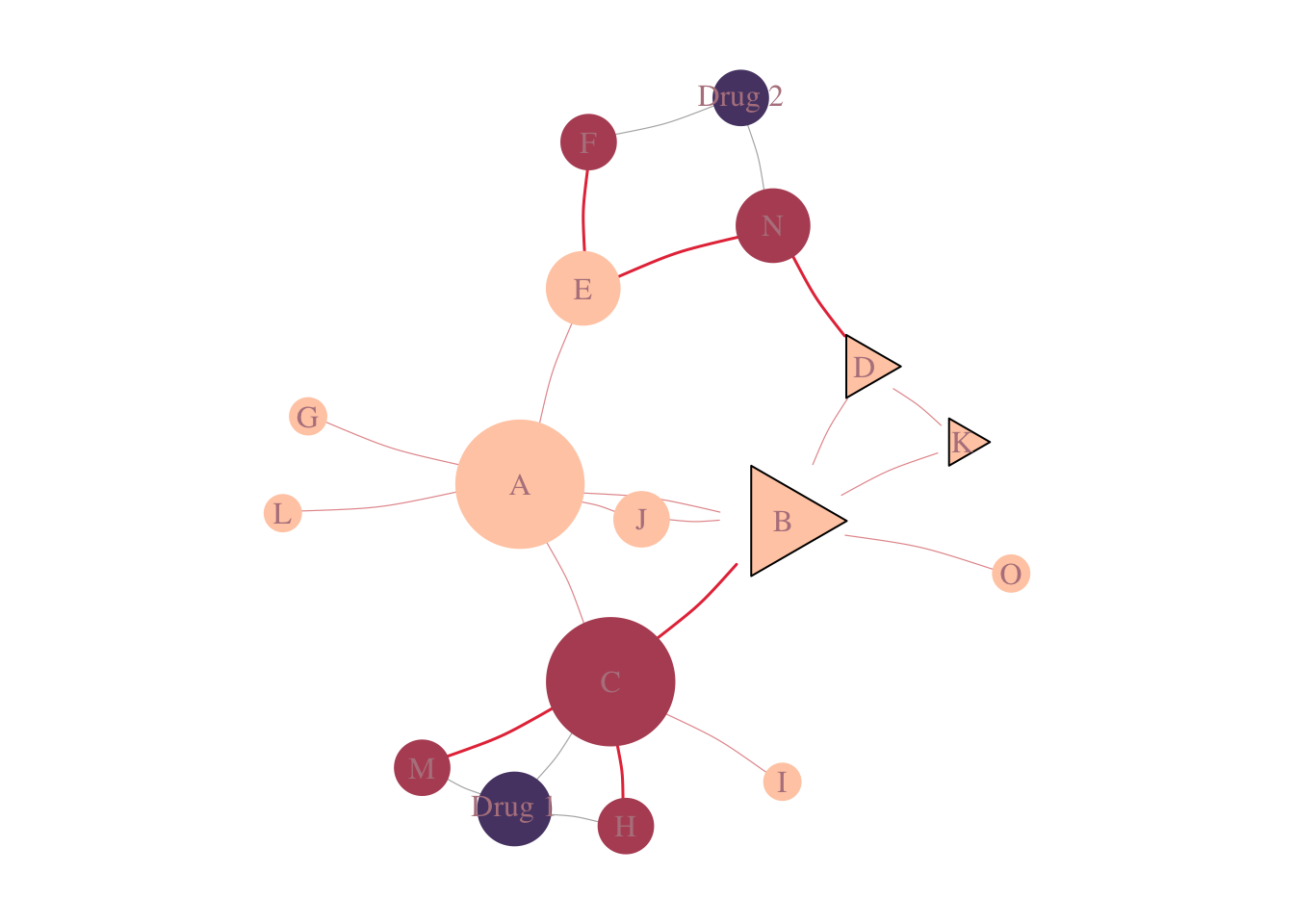
Figure 4.1: Drug-Target & Disease-Module Proximity. Triangles represent Disease Associated Genes, while circles represent non-associated genes. In dark purple, we see the drugs and light purple, its targets.
Similarly to the LCC (Session 3.1) it is important to calculate a measure of randomness associate to the proximity. In the same sense, it is important that the nodes being randomized, the nodes are not simply randomly selected from the pool of proteins in the PPI, but rather selected from matching degree proteins. To calculate the significance of the proximity one can calculate its Z-Score or simply calculate the empirical probability under the curve from the empirical distribution. Similarly, the Z-score is given by:
\[ Z-Score_{d(g,t)} = \frac{d(g,t) - \mu_{d(g,t)}}{\sigma_{d(g,t)}}. \]
4.2 Example in real data
Let’s try it to identify drugs that could work for our disease sets. Let’s focus on hyperlipidemia and focus on five drugs at first.
- Asenapine;
- Phentermine;
- Simvastatin;
- Pizotifen;
- Eprotirome.
hyperlipidemia_genes = Cleaned_GDA %>%
filter(diseaseName == 'hyperlipidemia') %>%
pull(geneSymbol) %>%
unique()
Asenapine_t = DT %>%
filter(Name == 'Asenapine') %>%
pull(Gene_Target)
Asenapine_t## [1] "HTR1A" "HTR1B" "HTR2A" "HTR2B" "HTR2C" "HTR5A" "HTR6" "HTR7"
## [9] "DRD2" "DRD3" "DRD4" "DRD1" "ADRA1A" "ADRA2A" "ADRA2B" "ADRA2C"
## [17] "HRH1" "HRH2" "ADRB1" "ADRB2" "UGT1A4" "CYP1A2" "CYP2D6" "CYP3A4"
## [25] "ALB" "ORM1"proximity_average(gPPI,
source = hyperlipidemia_genes,
targets = Asenapine_t)## [1] 1.961538Let’s do it in a loop:
drugs = c("Asenapine",
'Phentermine',
'Simvastatin',
'Pizotifen',
'Eprotirome')
p = list()
for(i in 1:length(drugs)){
d = drugs[i]
Drug_targets = DT %>%
filter(Name %in% d) %>%
pull(Gene_Target)
prox = proximity_average(gPPI,
source = hyperlipidemia_genes,
targets = Drug_targets)
p[[i]] = data.frame(prox = prox,
ntargets = length(Drug_targets),
drug = d)
}
p %<>% bind_rows()Now, let’s do the same, but also calculating the significance of the proximity.
Drug_Target = DT %>%
filter(Name %in% drugs) %>%
select(Name, Gene_Target) %>%
unique()
names(Drug_Target) = c('ID', "Target" )
proximity_significance = avr_proximity_multiple_target_sets(
set = drugs,
G = gPPI,
ST = Drug_Target,
source = hyperlipidemia_genes,
N = 1000,
bins = 100,
min_per_bin = 20
)##
|
| | 0%
|
|============== | 20%
|
|============================ | 40%
|
|========================================== | 60%
|
|======================================================== | 80%
|
|======================================================================| 100%Which are the drugs that we can use for hyperlipidemia?
proximity_significance## Drug targets targets_G proximity IC_97.5 IC_2.5 p_gt
## Asenapine Asenapine 26 26 1.961538 2.269231 1.923077 0.905
## Phentermine Phentermine 7 7 2.000000 2.860714 2.000000 0.952
## Simvastatin Simvastatin 20 19 2.157895 2.578947 2.103947 0.920
## Pizotifen Pizotifen 17 17 2.058824 2.295588 1.880882 0.642
## Eprotirome Eprotirome 2 2 1.500000 3.000000 1.000000 0.929
## p_lt Z
## Asenapine 0.095 -1.5969867
## Phentermine 0.048 -1.6491003
## Simvastatin 0.080 -1.6865893
## Pizotifen 0.358 -0.4609439
## Eprotirome 0.071 -1.4765928Now, let us check those drug indications:
Indication = DT %>%
filter(Name %in% drugs) %>%
select(Name, Indication) %>%
unique()
Indication## Name
## 1: Phentermine
## 2: Simvastatin
## 3: Eprotirome
## 4: Pizotifen
## 5: Asenapine
## Indication
## 1: Phentermine is indicated, alone or in combination with topiramate, as a short-term adjunct, not pass a few weeks, in a regimen of weight reduction based on exercise, behavioral modifications and caloric restriction in the management of exogenous obesity for patients with an initial body mass index (BMI) greater than 30 kg/m2 or greater than 27 kg/m2 in presence of other risk factors such as controller hypertension, diabetes or hyperlipidemia.[FDA label]\r\n\r\nExogenous obesity is considered when the overweight is caused by consuming more food than the person activity level warrants. This condition commonly causes an increase in fat storage. It is an epidemic condition in the United States where over two-thirds of adults are overweight or obese and one in three Americans is obese. In the world, the incidence of obesity has nearly doubled.[A174391]
## 2: Simvastatin is indicated for the treatment of hyperlipidemia to reduce elevated total cholesterol (total-C), low-density lipoprotein cholesterol (LDL‑C), apolipoprotein B (Apo B), and triglycerides (TG), and to increase high-density lipoprotein cholesterol (HDL-C).[F4655, F4658]\r\n\r\nThis includes the treatment of primary hyperlipidemia (Fredrickson type IIa, heterozygous familial and nonfamilial), mixed dyslipidemia (Fredrickson type IIb), hypertriglyceridemia (Fredrickson type IV hyperlipidemia), primary dysbetalipoproteinemia (Fredrickson type III hyperlipidemia), homozygous familial hypercholesterolemia (HoFH) as an adjunct to other lipid-lowering treatments, as well as adolescent patients with Heterozygous Familial Hypercholesterolemia (HeFH).[F4655, F4658]\r\n\r\nSimvastatin is also indicated to reduce the risk of cardiovascular morbidity and mortality including myocardial infarction, stroke, and the need for revascularization procedures. It is primarily used in patients at high risk of coronary events because of existing coronary heart disease, diabetes, peripheral vessel disease, history of stroke or other cerebrovascular disease.[F4655, F4658]\r\n\r\nPrescribing of statin medications is considered standard practice following any cardiovascular events and for people with a moderate to high risk of development of CVD. Statin-indicated conditions include diabetes mellitus, clinical atherosclerosis (including myocardial infarction, acute coronary syndromes, stable angina, documented coronary artery disease, stroke, trans ischemic attack (TIA), documented carotid disease, peripheral artery disease, and claudication), abdominal aortic aneurysm, chronic kidney disease, and severely elevated LDL-C levels.[A181087, A181406]
## 3: Investigated for use/treatment in hyperlipidemia, metabolic disease, and obesity.
## 4: Indicated for the prophylactic management of migraines [L2292].
## 5: Used for treatment in psychosis, schizophrenia and schizoaffective disorders, manic disorders, and bipolar disorders as monotherapy or in combination.4.3 Exercises
Test the same drugs for all the five other diseases we are interested. How do those values compare?
- Autistic Disorder;
- Obesity;
- Hyperlipidemia;
- Rheumatoid Arthritis.
Choose one disease and visualize the disease module along with each of the drugs we tested.